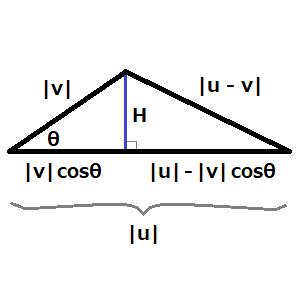
◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇

ベクトルの内積を証明している自分の観察

発行：エスオーエル株式会社
https://www.sol-j.co.jp/

連載「X線CTで高精度寸法測定！？」
2022年5月11日号　VOL.135

平素は格別のお引き立てを賜り、厚く御礼申し上げます。
X線CTによる精密測定やアプリケーション開発情報などをテーマに、
無料にてメールマガジンを配信いたしております。

◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇◆◇



前回は、平行六面体に関するベクトルの計算をしました。
今回は、それに関連して、ベクトルの内積の証明を書こうと思いました。

ベクトル a = (a1, a2, a3) と b = (b1, b2, b3) が与えられたとき、
その内積 a・b は、成分を使って、

　　a・b = a1 b1 + a2 b2 + a3 b3

と書けます。
一方で、ベクトルの成す角度を θ とすると、

　　a・b = ｜a｜｜b｜cosθ

と書けます。
つまり、

　　｜a｜｜b｜cosθ = a1 b1 + a2 b2 + a3 b3

を証明しようと思ったのです。

ベクトルの内積は、今でも結構頻繁に使います。
この証明もこれまでの人生で何回もやりました。

そして、記事を書くために、証明を書いてみようとすると、
「幸運にも」証明のやり方を忘れていることに気付きました。

内積を日頃当たり前のように使っているので、
過去に証明して納得していることを毎回証明し直すことはないため、
証明の手順をすっかり忘れていました。


　　忘れた証明をやり直すと、
　　初めて証明できたときと同じような達成感
　　をもう一度味わえます。

　　そしてもう一つ、脳の活動の観察という
　　個人的な趣味の良い題材になるのです。
　　「今これは、記憶にアクセスしているのか」とか、
　　「記憶ではなく閃きが来たのか」とか
　　を俯瞰的に観察するのです。

　　小さい子供の頃から自分の脳の活動の観察という趣味(?)があり、
　　「記憶する」「忘れる」「神経回路がつながった感触」
　　「気づいている状態」「集中状態」等をよく観察していました。

　　観察している状態の観察が特に面白く、
　　観察していない状態は観察できないので、
　　観察していなかった状態の直後の観察がさらに面白いのです。


　　　　何を言っているのか分らないかもしれませんが、
　　　　これを理解してくれて、同じ経験をしている人が
　　　　一定数居るということを大人になってから知り、
　　　　さらに深く継続しているのです。


　　この趣味に、数学がとてもよく合うということに気づいてから、
　　数学をよくやるようになりました。小学生の頃です。
　　（数学という趣味の方が後でした。）

　　丸暗記の証明を再現するのと、
　　過去にやったけどうろ覚えの証明をやり直すのと、
　　過去にやったけど全然覚えていない証明に挑戦するのと、
　　初めての証明に挑戦するのとでは、
　　どれも脳の働き方が違います。

　　証明に取り組んでいる最中の脳の働きも違いますし、
　　終えた後の達成感や満足感も微妙に違います。
　　
　　ちなみに、達成感と満足感もほぼ同時に来ますが、
　　それぞれ感覚が違います。持続時間も違います。
　　このような観察が楽しいのです。
　　（たぶん、脳内物質の種類や量や滞在時間の違いです。）


さて、パッと見た感じ、ベクトル a の成分の二乗和の平方根と
ベクトル b の成分の二乗和の平方根を掛けて、
さらに cosθ を掛けたものが、
ベクトルの第j成分同士の掛け算の和と等しい
という式が簡単に見えないため、ワクワクしましたが、

三角形を描いて、垂線を引いて、愚直に計算すると
すぐに証明できました。

記事としては、つまらないかもしれないと思いつつ、
でも「内積」は奥が深いから、その証明に関連して、
いろいろ思うところを書こうと思いました。

しかし、記事を書く準備ができた後に、
書こうとしていたネタで2014年に既に記事を
書いていたことに気づきました。
まったく忘れていました。

　　A-0041. 内積の定義とちょっとした計算


とても残念だったので、
「平行六面体の体積と外積」というタイトルで
今回の記事を書き始めたのですが、

タイトル変更の経緯を書いているうちに、
このような訳の分からない記事になってしまい、

タイトルも、さらに
「ベクトルの内積を証明している自分の観察」
と変更することになりました。

このようなことを書いている時点で、
メタ的思考の持ち主で、観察が趣味という
性質が表れています。（という観察をしています。）

外積については、次回に書こうと思います。


最後に、2014年の記事で省略した証明部分の
図と計算を載せておきます。

青い垂線は、左の直角三角形と右の直角三角形から、
長さ H がそれぞれ、

　　H^2 = |v|^2 - (|v| cosθ)^2

　　H^2 = |u - v|^2 - (|u| - |v| cosθ)^2

と書けるので、

　　|v|^2 - (|v| cosθ)^2 = |u - v|^2 - (|u| - |v| cosθ)^2

を展開して、整理すると、

　　|v-u|^2 = |u|^2 + |v|^2 - 2|u||v| cosθ

を得ます。
（θ>90° のときも、図と計算が少し変わりますが、同様に確認できます。）


--
高野智暢